Sum Check Protocol - part 2: Triangle counting

To understand how the triangle counting can be represented by a polynomial, which is the form the sum check protocol described in Sum check - overview requires, it would be helpful to understand how the triangles can be represented using a adjacency matrix beforehand. The intuition around its matrix representation is fundamental to understanding its polynomial form from my view.

This post focuses explaining how to counting triangles in adjacency matrix, laying down the connection to the Sum check - benchmarks in which triangle counting will be applied into sum check protocol.

Below outlines the features of triangle counting using operations under matrix structure.

Overview

Adjacency matrix is an representation of undirected graph to denote relationship between vertices and edges.

Before we dive into understanding how the graph works at low level, here are some high level implications for the triangle counting use case.

• The graph by an adjacency matrix by itself represents one walk between vertices.
• Having an adjacency matrix multiplied with itself, resulting in $A^2$, it is representing two walks between vertices.
• Multiplying itself two times, resulting in $A^3$, it is representing three walks between vertices.
• The values in the trace of the resulted matrix $A^3$ are the number of round trips. Summing them up and divide by 6, equals to the total number of triangles that can be found in the graph. The following will try to explain why it is the number 6.

Representation

Firstly, let's take a look at the polynomial representing triangle counting.

But what does this polynomial implies? What does $f_A$ means? What do $x,y,z$ variable represent?

To clarify these questions, it would be helpful to take a look at the following examples of what they represent for $A$, $A^2$ and $A^3$ respectively.

Trips of $A$

This represents the counts of trips having one walk.

$A$ can be represented as the function $f_A(x,y)$ for the following mappings with one walk paths.
$(x=1,y=2)\Rightarrow (1\to 2)$
$(x=1,y=3)\Rightarrow (1\to 3)$
$(x=2,y=3)\Rightarrow (2\to 3)$
$(x=2,y=4)\Rightarrow (2\to 4)$
$(x=3,y=4)\Rightarrow (3\to 4)$

Corresponding, the following graph illustrates one walk paths.

flowchart LR
   1 --> 2 & 3
   2 --> 4
   2 --> 3
   3 --> 4

Since the adjacency matrix is symmetry, so the arrow directions can be reversed.

Trips of $A^2$

This represents the counts of trips having two walks.

Round trip example

$A^2$ can be represented as the function $f_A(x,y)\cdot f_A(y,z)=f_A(x,z)$ for the following mappings with two walk paths.

$f_A(x,y)$
$(x=1,y=2)\Rightarrow (1\to 2)$
$(x=1,y=3)\Rightarrow (1\to 3)$

$f_A(y,z)$
$(y=2,z=1)\Rightarrow (2\to 1)$
$(y=3,z=1)\Rightarrow (3\to 1)$

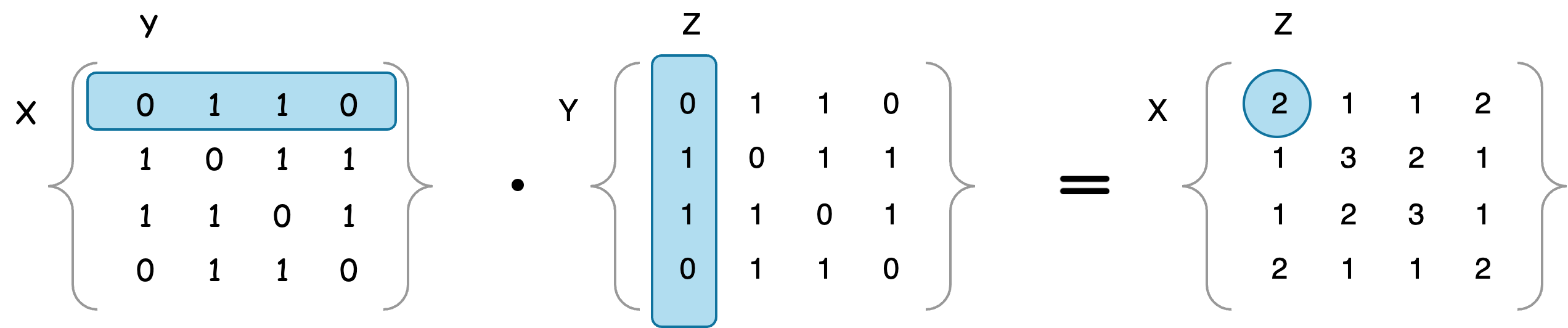
Corresponding, the following graph illustrates two walk paths for $f_A(x,y)\cdot f_A(y,z)$.

flowchart LR
   1 --> 2 & 3--> 1

The example above also can be represented by $\sum _{(x=1,1\le y\le 4,z=1)}{f}_A(x,y)\cdot f_A(y,z)$. We can see there are 2 paths for round trips, and the result is denoted in the $f_A(x,z)$ where $x=1,z=1$, which is a point in the matrix trace.

Intermediate trip example

The values other than the ones from the trace of the matrix represent the number intermediate trips, instead of round trips.

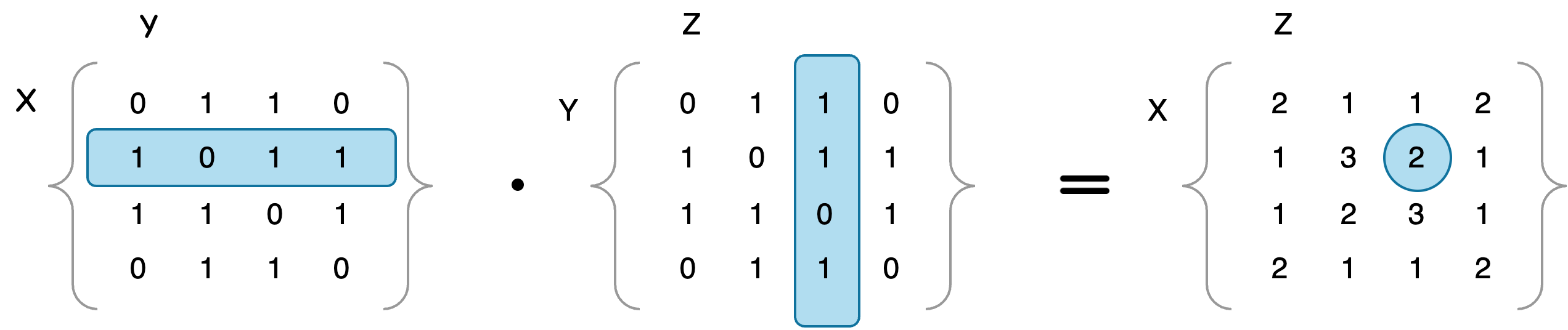
For point $(2,3)$ in $A^2$, that is $f_{A^2}(2,3)=\sum _{(x=2,1\le y\le 4,z=3)}{f}_A(x,y)\cdot f_A(y,z)$, there are 2 trips involves two walks as below.

flowchart LR
   2 --> 1 & 4--> 3

Trips of $A^3$

This represents the number of trips having three walks. When it is a count for round trip, the value in the trace of $A^3$, it represents the number of triangle, starting from a vertice.

Round trip example

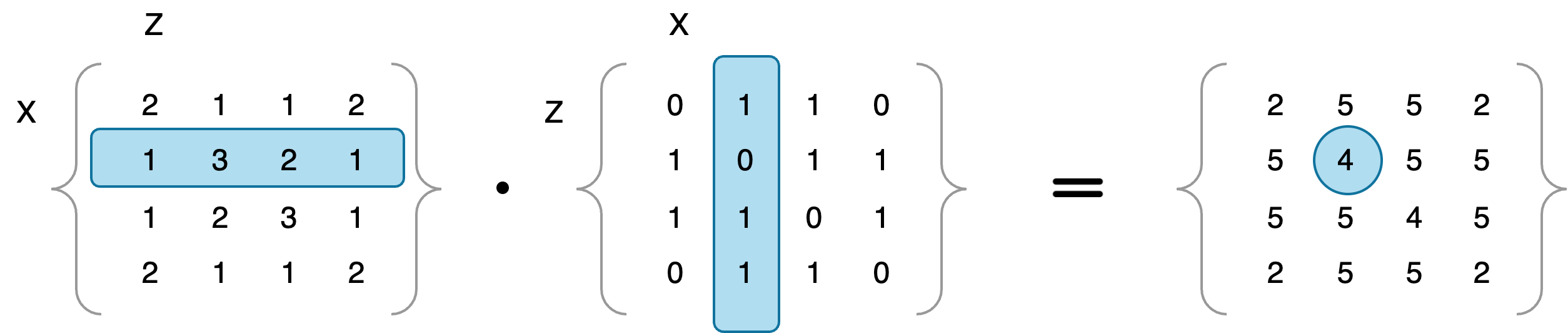
For the point $(2,2)$ in $A^3$, that is $f_{A^3}(2,2)=\sum _{(x=2,1\le z\le 4)}{f}_{A^2}(x,z)\cdot f_A(z,x)$, there are 3 round trips involves three walks as below.

flowchart LR
   2 --> 1 & 3 & 4--> 2

Seemingly, there only 3 round trips with two walks around vertice 2. But keep in mind the $f_{A^2}$ represents two walk trips, which can be expanded in a graph.

With the trips represented by $f_{A^2}$ expanded between the vertices 2 and 3, the following two triangles can be formed, as the there are 2 intermediate trips represented by $f_A^2(2,3)\cdot f_A(3,2)$

flowchart LR
   2 --> 1 --> 3 --> 2

flowchart LR
   2 --> 4 --> 3 --> 2

With $f_{A^2}(2,1)\cdot f_A(1,2)$ expanded

flowchart LR
   2 --> 3 --> 1 --> 2

With $f_{A^2}(2,4)\cdot f_A(4,2)$ expanded

flowchart LR
   2 --> 3 --> 4 --> 2

Thus, there are total 4 undirected round trips as the $f_{A^3}(2,2)$ denotes.

Matrix trace

Based on the method we observed in counting the round trips, to calculate the total number of triangles, it just need to sum up the values in the trace of $A^3$ as the result $C$.

Because the adjacency matrix in our example is symmetry, so is undirected. The result $C$ must be divided by 2. Also the triangle paths can start from any one of the 3 vertices and the paths will be redundant for counting a triangle. So the result $C$ also needs to be divided by 3. Therefore, it needs to be divided by 6.

Into polynomial

The implication of summing up the trace values of matrix multiplication result $A^3$ means counting round trips with 3 walks through the paths between vertices $(x,y,z)$. Intuitively, the triangle counting can then be represented by a polynomial form

In the Sum check - benchmarks, we will explain how this polynomial can be applied to the sum check protocol.